Working Groups / Numerical Modelling

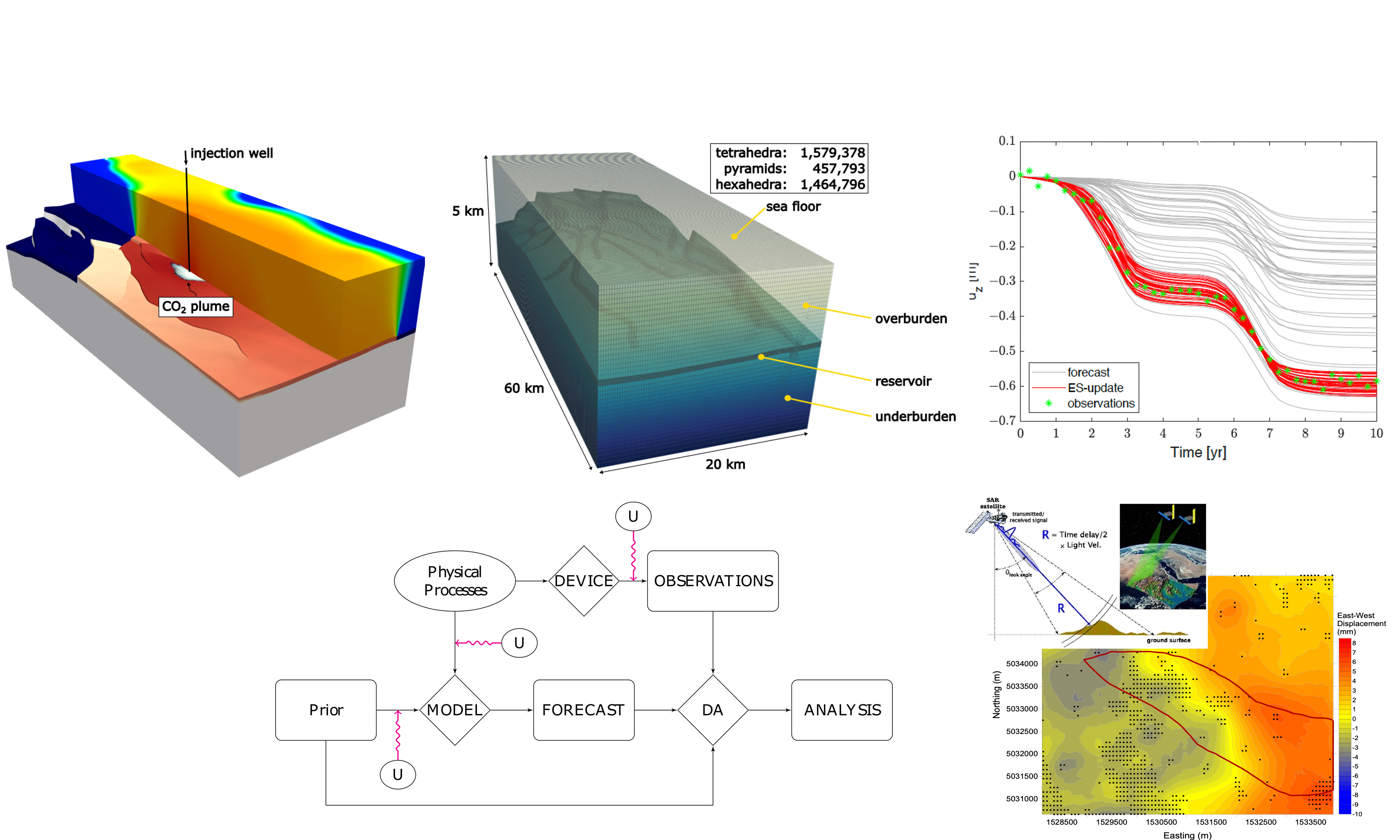
Model predictions can be more or less reliable, making it essential to quantify their associated uncertainty. For example, when studying subsidence in the Po River delta using a numerical model, the predicted surface lowering depends on input data, such as subsurface geology and lithology. Additional uncertainty arises from the simplifications inherent in modeling complex systems. Finally, observations used for model calibration and validation also introduce errors. Overall, the final prediction reflects the combined uncertainty from data, model assumptions, and measurements, highlighting the need for a probabilistic analysis for proper interpretation.

Natural phenomena are described by scientists through mathematical models, which allow predicting the future behavior of a system. A classic example is the principle of action and reaction. When the equations are too complex for a direct solution, numerical models, such as the finite element method, are used to approximate the solution. Subsidence, a phenomenon related to the deformation of the free surface, is governed by the same equations that describe a body in equilibrium. The variation in the pressure of the interstitial fluid causes deformation of the medium, which can be described using constitutive laws, such as the linear elastic law.